I don’t know if I can tell if this function is bugged or what, but I want to discuss this _bankers_rounding_legacy function frappe v14.27.1
The code is written from frappe v14.27.1 in utils/data.py
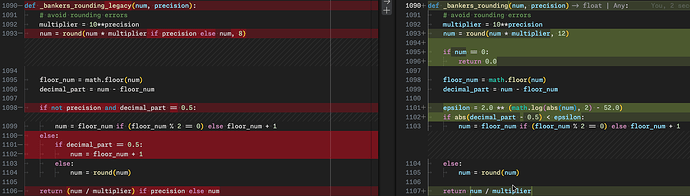
def _bankers_rounding_legacy(num, precision):
# avoid rounding errors
multiplier = 10**precision
num = round(num * multiplier if precision else num, 8)
floor_num = math.floor(num)
decimal_part = num - floor_num
if not precision and decimal_part == 0.5:
num = floor_num if (floor_num % 2 == 0) else floor_num + 1
else:
if decimal_part == 0.5 :
num = floor_num + 1
else:
num = round(num)
return (num / multiplier) if precision else num
I notice when I create a return, for example, the vat is - 28.875 ( the - because it is a return )
The values will be like this.
num=-2887.5
floor_num=-2888
decimal_part=0.5
so when we reach
if decimal_part == 0.5 :
num = floor_num + 1 that equal to -2888 + 1 = -2887
So the vat will be rounded to 2 decimal points and will be -28.87
On the other hand, my code in v13 (I added two lines to the production version ) and the function named rounded on utils.data
multiplier = 10**precision
# print("multiplier = "+str(multiplier)+"\n precision = "+str(precision))
# avoid rounding errors
num = round(num * multiplier if precision else num, 8)
floor_num = cint(num)
decimal_part = num - floor_num
if not precision and decimal_part == 0.5:
num = floor_num if (floor_num % 2 == 0) else floor_num + 1
else:
if decimal_part == 0.5 :
num = floor_num + 1
elif decimal_part == -0.5:
num=floor_num-1
else:
num = round(num)
return (num / multiplier) if precision else num
Let’s apply the same value here -28.875
num=-2887.5
floor_num=-2887
decimal_part=-0.5
so when we reach
elif decimal_part == -0.5 :
num = floor_num - 1 that equal to -2887 - 1 = -2888
So the vat will be rounded to 2 decimal points and will be -28.88
After these mathematics, let’s return to the invoice I created the return from it. The vat will be 28.875
if we apply both codes, the value will be
num=2887.5
floor_num=2887
decimal_part=0.5
so when we reach
if decimal_part == 0.5 :
num = floor_num +1 that equal to 2887 + 1 = 2888
So the vat will be rounded to 2 decimal points and will be 28.88
If we apply a return on the first code, the sales invoice will have an outstanding amount of 0.01 because 28.88 - 28.87 = 0.01
in the end, sorry for the extended topics, and I hope you understand me correctly,
but now is _bankers_rounding_legacy bugged, or do I misunderstand how the default of bankers_rounding_legacy method works